IDENTIDADES FUNDAMENTALES EN LAS RAZONES TRIGONOMÉTRICAS

Una identidad trigonométrica es una igualdad entre expresiones que contienen funciones trigonométricas y es válida para todos los valores del ángulo en los que están definidas las funciones (y las operaciones aritméticas involucradas).

IDENTIDADES BÁSICAS  

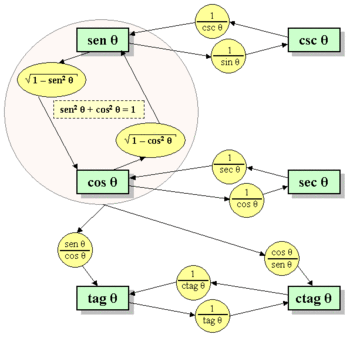
sen² β + cos² β =1

sen ² 30+ cos² 30=1

sen² 60 + cos² 60 =1

sen² 45 + cos² 45= 1

EJEMPLO:sen² 30 = cos² 30 =1
(1/2)(1/2)² + (√3/2)² = 1
1/4 + 3/4 =1
4/4 = 1
1 = 1
sen β       =    1/cos β               cos β ≠ 0
cosc β     =    1/senβ               sen β ≠ 0
cotan β    =    1/tanβ               tan β  ≠ 0
tan β        =    sen β/ cos β      cos β  ≠ 0
cotan β    =    cos β /senβ       sen β ≠ 0
tan  β       =    1/cat β