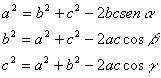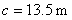GRÁFICA DE LA FUNCIÓN SENO EN CABRI 
INSTRUCCIONES PARA SU CONSTRUCCIÓN

Despues de la experimentación y el seguimiento de las instrucciones del tutor en el programa cabri la grafica de la funcion seno queda de la siguiente manera:

En el primer cuadrante 

EN EL SEGUNDO CUADRANTE

EN EL TERCER CUADRANTE

 EN EL CUARTO CUADRANTE

 Y FINALMENTE AL COMPLETAR EL CICLO NUMERO 1 DE LA FUNCIÓN SENO ESTA PUEDE SEGUIRSE EXTENDIENDO MAS

Este programa Cabri es de gran ayuda en el manejo de graficas de funciones trigonométricas y así comprobar las gráficas con el uso de la tecnología y la evolución del hombre 

FUNCIONES EN EL PLANO CARTESIANO 

Una función :

El concepto de función matemática o simplemente función, es sin duda, el más importante y utilizado en Matemáticas y en las demás

ramas de la Ciencia. No fue fácil llegar a él y muchas mentes muy brillantes han dedicado enormes esfuerzos durante siglos para que tuviera

una definición consistente y precisa.

Desde los tiempos de Galileo, que fue uno de los primeros en usarlo (aunque no en la forma que nosotros lo conocemos actualmente),

pasando por el gran Newton y Leibniz, que fue el primero que en 1673 usó la palabra "función" para referirse a la relación de dependencia de

dos variables o cantidades, Euler, que le dio su formulación moderna y = f(x), Cauchy, Dirichlet o Gauss, las mejores mentes de la Historia

de la Humanidad le dedicaron su atención y sus desvelos.

FUNCIÓN SENO 

f(x) = sen x

La función seno asocia a cada número real, x, el valor del seno del ángulo cuya medida en radianes es x.

Dominio: Reales

Rango: [-1.1]

Periodo : 2pi rad

FUNCIÓN COSENO 

f(x) = cosen x

La función coseno asocia a cada número real, x, el valor del coseno del ángulo cuya medida en radianes es x.

Dominio: Reales

Rango : [-1,1]

Periodo: 2pi rad 

SENO Y COSENO 

FUNCIÓN TANGENTE

Sea A un ángulo agudo de un triángulo rectángulo. La tangente del ángulo A es el cociente entre el cateto opuesto BC y el adyacente AB.
La tangente es sobreyactiva Nunca se corta.
Dominio: Reales
Rango: Reales negativos y reales positivos Va desde el limite del infinito hasta el infinito 
Perido: pi rad 
Siempre es creciente 

RAZONES TRIGONOMÉTRICAS PARA ÁNGULOS EN POSICIÓN NORMAL 

• Ángulo en Posición Normal :Llamado también ángulo en posición canónica o estándar; es aquel ángulo trigonométrico cuyo vértice coincide con el origen del sistema cartesiano, su lado inicial coincide con el semieje positivo de abscisas y su lado se ubicará en cualquier región del plano, siendo el que indique a que cuadrante pertenece dicho ángulo

 Ángulos Cuadrantales

Se va a denominar ángulo cuadrantal a aquel ángulo en posición normal cuyo lado final coincide con cualquiera de los semiejes cartesianos. Las medidas de estos ángulos es siempre múltiplo de 90º.

Estos ángulos no pertenecen a cuadrante alguno (fig. 1)

• Ángulos Coterminales 

Son aquellos ángulos en posición normal que tienen el mismo lado final; y su diferencia de medidas es siempre múltiplo de 360º. (fig.2).

• Definición de las razones trigonométricas de un ángulo en Posición Normal

Para definir o hallar las R.T. de un ángulo en posición normal; se debe conocer un punto perteneciente a su lado final.

En el gráfico; para "a"; tendremos:

Por ejemplo:

Se debe notar que ahora las R.T. pueden tener signo negativo; dependiendo del cuadrante en el que se ubique el ángulo considerado.

Dependiendo del cuadrante en que se ubiquen las funciones podremos definir los signos de estas. Así:

En el primer cuadrante : Todas las funciones son positivas

En el segundo cuadrante: El sen y csc positivas El resto son negativas

En el tercer cuadrante: Tan y Cotan son positivas el resto son negativas

En el cuarto cuadrante: Cos y Sen son positivos el resto son negativos 

LEY DE COSENOS 

La ley de cosenos se puede considerar como una extención del teorema de Pitagoras aplicable a todos los triángulos.  Ella enuncia así: el cuadrado de un lado de un triángulo es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de estos dos lados multiplicado por el coseno del ángulo que forman.  Si aplicamos este teorema al triángulo de la figura 1 obtenemos tres ecuaciones: La expresión "resolver el triangulo" significa hallar cada uno de los valores de sus lados y la medida de sus ángulos. Para resolver triángulos rectángulos se utiliza la ley del seno y/o la del coseno EJEMPLO: Supongamos que en el triángulo de la figura 1 . Encontrar la longitud del tercer lado. Solución: Para calcular el valor del tercer lado, podemos emplear la ley de cosenos: De esta misma manera podemos hallar la medida de los otros lados y de sus ángulos solo aplicando la formula de la ley de cosenos de una forma fácil

LEY DE LOS SENOS 

La ley de los Senos es una relación de tres igualdades que siempre se cumplen entre los lados y ángulos de un triángulo cualquiera, y que es útil para resolver ciertos tipos de problemas de triángulos.

La ley de senos nos dice que la razón entre la longitud de cada lado y el seno del ángulo opuesto a el en todo triángulo es constante.Si observamos la figura 1, la ley de senos se escribirá como sigue:

FIGURA 1 

Resolución de triángulos por la ley de los Senos

Resolver un triángulo significa obtener el valor de la longitud de sus tres lados y la medida de sus tres ángulos internos.

Para resolver triángulos que nos son rectángulos se utiliza la ley de senos y/o la ley de cosenos  Todo dependerá de los valores conocidos.

Ejemplo:

Supongamos que en el triángulo de la figura 1 . Encontrar la longitud del del tercer lado y la medida de los otros dos ángulos.

Solución:

Calculemos el ángulo 

9.30 m/sen  30.8 = 5.40m/sen β

sen β = 5.40 sen 30.8 /9.30

β = 17.3º 

Con los angulos interiores de un angulo debemos sumar 180º y asi obtener el angulo r

                                                     r = 180º - (α+β) 

                                                     r = 180º - (30.8º + 17.3º )

                                                     r= 132º 

 Finalmente para poder calcular el lado c podemos usar nuevamente la ley de los senos 

                                                  c/sen r = a/ sen α 

                                                  c = 9.30m sen 132º/ sen 30.8º 

                                                  c = 13.6m 

De esta manera gracias ala ayuda de la ley de los senos podemos solucionar triángulos utilizando diferentes razones y funciones trigonométricas y de una manera mas fácil y útil así como corta 

IDENTIDADES FUNDAMENTALES EN LAS RAZONES TRIGONOMÉTRICAS

Una identidad trigonométrica es una igualdad entre expresiones que contienen funciones trigonométricas y es válida para todos los valores del ángulo en los que están definidas las funciones (y las operaciones aritméticas involucradas).

IDENTIDADES BÁSICAS  

sen² β + cos² β =1

sen ² 30+ cos² 30=1

sen² 60 + cos² 60 =1

sen² 45 + cos² 45= 1

EJEMPLO:sen² 30 = cos² 30 =1
(1/2)(1/2)² + (√3/2)² = 1
1/4 + 3/4 =1
4/4 = 1
1 = 1
sen β       =    1/cos β               cos β ≠ 0
cosc β     =    1/senβ               sen β ≠ 0
cotan β    =    1/tanβ               tan β  ≠ 0
tan β        =    sen β/ cos β      cos β  ≠ 0
cotan β    =    cos β /senβ       sen β ≠ 0
tan  β       =    1/cat β       

RAZONES TRIGONOMÉTRICAS PARA ÁNGULOS NOTABLES 

Aquí vemos las razones trigonométricas de los ángulos especiales: 

A continuación le mostramos ejemplos de las razones trigonométricas:

  

EJEMPLO

Dos personas A y B separadas por "a" metros observan el campanario de una iglesia, como lo muestra la figura de abajo. A observa con un ángulo de elevación del 60º y B lo observa con un ángulo de elevación de 45º. ¿Cuál es la altura del campanario?

Respuesta:

  

Finalmente vamos a poner un cuadro con la razón fundamental trigonométrica:

Sen2 (x) + cos2 (x) =1